Câu hỏi:
13/07/2024 39,868
Cho ∆ABC đem AB = 2, AC = 3, \(\widehat A = 60^\circ \). Tính chừng nhiều năm phân giác \(\widehat A\).
Trả lời:
![]()
Giải tự Vietjack
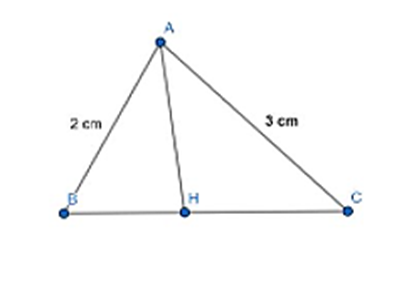
Áp dụng tấp tểnh lí hàm số côsin mang đến ∆ABC tao có: \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.cos60^\circ = \sqrt 7 \)
Gọi AH là đàng phân giác góc A.
Áp dụng đặc thù đàng phân giác mang đến ∆ABC: \(\frac{{AB}}{{AC}} = \frac{{BH}}{{HC}}\)
\(\frac{{AB}}{{BH}} = \frac{{AC}}{{HC}} = \frac{{AB + AC}}{{BH + HC}} = \frac{{2 + 3}}{{BC}} = \frac{5}{{\sqrt 7 }}\)
\( \Rightarrow BH = AB:\frac{5}{{\sqrt 7 }} = \frac{{2\sqrt 7 }}{5}\)
\(\cos \widehat B = \frac{{A{C^2} - A{B^2} - B{C^2}}}{{ - 2AB.BC}} = \frac{{\sqrt 7 }}{{14}}\)
Xét ∆ABH có: \(A{H^2} = A{B^2} + B{H^2} - 2.AB.BH.cos\widehat B = \frac{{108}}{{25}} \Rightarrow AH = \frac{{6\sqrt 3 }}{5}\).
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho \(\cos x = \frac{2}{{\sqrt 5 }},0 < x < \frac{\pi }{2}\). Tính những độ quý hiếm lượng giác của góc x.
Câu 2:
Cho ∆ABC đem \(\frac{5}{{\sin A}} = \frac{4}{{\sin B}} = \frac{3}{{\sin C}}\) và a = 10. Tính chu vi tam giác.
Câu 3:
Cho tana = 2. Tính độ quý hiếm của biểu thức \(C = \frac{{\sin a}}{{{{\sin }^3}a + 2{{\cos }^3}a}}\).
Câu 4:
Trên khoảng chừng \(\left( {\frac{\pi }{2};2\pi } \right)\), phương trình \(\cos \left( {\frac{\pi }{6} - 2\pi } \right) = \sin x\) đem từng nào nghiệm ?
Câu 5:
Cho ∆ABC. Gọi M, N, Phường thứu tự là trung điểm những cạnh AB, AC, BC. Hỏi \(\overrightarrow {MP} + \overrightarrow {NP} \) tự vectơ nào?
Câu 6:
Chứng minh rằng: \(\frac{{1 + \cot x}}{{1 - \cot x}} = \frac{{\tan x + 1}}{{\tan x - 1}}\).
Bình luận
Hãy Đăng nhập hoặc Tạo thông tin tài khoản nhằm gửi comment
Bình luận
🔥 Đề đua HOT:
