Câu hỏi:
12/07/2024 105,533
Trả lời:
![]()
Giải vì chưng Vietjack
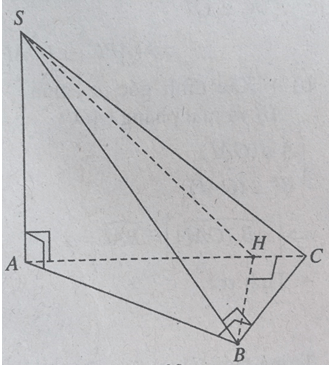
a) BC ⊥ SA và BC ⊥ AB) ⇒ BC ⊥ (SAB)
⇒ BC ⊥ SB.
⇒ tam giác SBC vuông bên trên B.
b) BH ⊥ AC và BH ⊥ SA ⇒ BC ⊥ (SAC)
⇒ (SBH) ⊥ (SAC).
c) d[B, (SAC)] = BH. Ta có:
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp tứ giác đều S.ABCD. Gọi M, N theo lần lượt là trung điểm của SA và SC.
a) Chứng minh AC ⊥ SD
b) Chứng minh MN ⊥ (SBD)
c) Cho AB = SA = a. Tính coossin của góc thân mật (SBC) và (ABCD)
Câu 2:
Cho hình chóp S.ABCD với lòng ABCD là hình vuông vắn cạnh vì chưng a và SA ⊥ (ABCD).
a) Chứng minh BD ⊥ SC.
b) Chứng minh (SAB) ⊥ (SBC).
c) Cho SA = (a√6)/3. Tính góc thân mật SC và mặt mũi phẳng phiu (ABCD).
Câu 3:
Cho tứ diện O.ABC với OA, OB, OC song một vuông góc và những cạnh OA = OB = OC = a, gọi I là trung điểm BC.
a) Chứng minh rằng: BC ⊥ (AOI), (OAI) ⊥ (ABC).
b) Tính góc thân mật AB và mặt mũi phẳng phiu (AOI).
c) Tính góc trong số những đường thẳng liền mạch AI và OB.
Câu 4:
Cho hình chóp S.ABCD, lòng ABCD là hình thoi cạnh a, , SA = SB = SD = a.
a) Chứng minh (SAC) vuông góc với (ABCD).
b) Chứng minh tam giác SAC vuông.
c) Tính khoảng cách kể từ S cho tới (ABCD).
Bình luận
Hãy Đăng nhập hoặc Tạo thông tin tài khoản nhằm gửi phản hồi
Bình luận