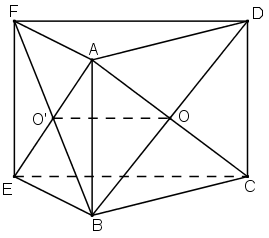
a) Do những tứ giác ABCD và ABEF là những hình bình hành
=> O là trung điểm của AC và BD
và O’ là trung điểm của AE và BF. (tính hóa học hình bình hành).
+ ΔBFD sở hữu OO’ là đàng tầm nên OO’ // DF
mà DF ⊂ (ADF)
⇒ OO' // (ADF)
+ ΔAEC sở hữu OO’ là đàng tầm nên OO’ // EC
mà EC ⊂ (BCE)
⇒ OO’ // (BCE).
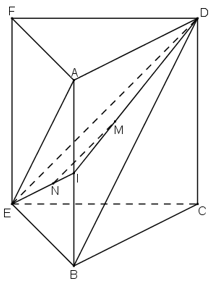
b)
Ta thấy mp(CEF) đó là mp(CEFD).
Gọi I là trung điểm của AB:
+ M là trọng tâm ΔABD
⇒ IM/ ID = 1/3.
+ N là trọng tâm ΔABE
⇒ IN/IE = 1/3.
+ ΔIDE sở hữu IM/ID = IN/IE = 1/3
⇒ MN // DE tuy nhiên ED ⊂ (CEFD)
nên MN // (CEFD) hoặc MN // (CEF).
Câu 1:
Cho tứ diện ABCD. Gọi M, N, Phường theo thứ tự là trung điểm của AB, AC, AD. Các đường thẳng liền mạch MN, NP, PM sở hữu tuy vậy song với mặt mũi phẳng lặng (BCD) không?